Cómo interactúan los errores alfa y beta

Dada una distribución de probabilidades determinada, los errores alfa y beta se mueven en sentido inverso. Veamos ejemplos.

En la figura 1 hay 2 distribuciones de probabilidad de medias que no se superponen en lo absoluto; es claro entonces que un valor de cualquiera de ellas no puede corresponder a la otra, y por lo tanto la diferencia estadística es clara. No hay dudas.

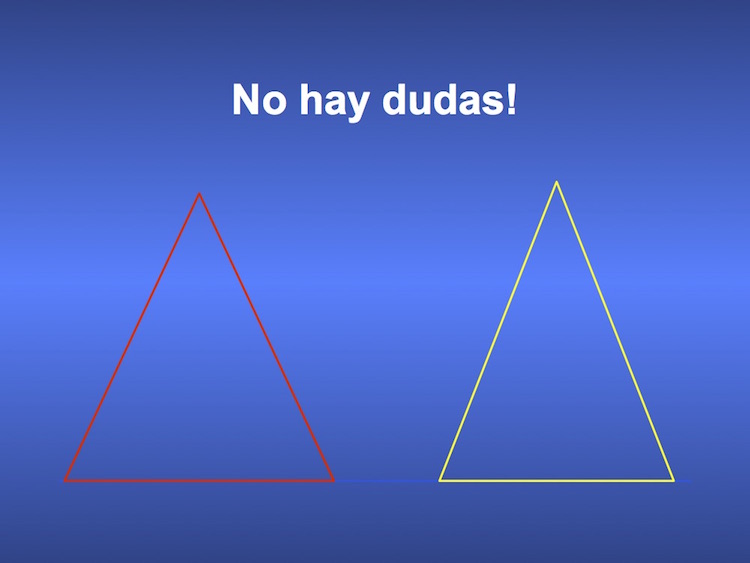
¿Pero qué sucede si hay superposición de ambas distribuciones? Es claro que de acuerdo a cuál sea el valor de corte definido habrá mayor o menor probabilidad de error alfa y beta, y por lo tanto sensibilidad y especificidad cambiantes para detectar la diferencia.

Supongamos una distribución de valores de creatinina plasmática de personas sanas, cuya media es 1 mg% (distribución A, en rojo en la figura), y otra distribución de valores de creatinina plasmática en hipertensos con cierto daño renal, cuya media es 1.5 mg% (distribución B, en amarillo en la figura). Veremos 3 casos.

En el caso 1 (figura 2) hemos decidido que el valor de corte de creatinina para definir daño renal, es 1,35 mg%, entendiendo que ello corresponde al 5% de valores más extremos y por lo tanto “patológicos” Como vemos en la figura, existe un área de la distribución A, rayada en blanco, con valores iguales o mayores a 1,35 mg%. Son valores de personas sanas, que por el valor de corte elegido consideraremos como correspondientes a personas “enfermas”. ¿Cuántas veces nos equivocaremos entonces, rechazando la hipótesis nula y pensando que existe una diferencia que no es tal, ya que se debe al azar, al atribuir un valor de 1,35 mg% o mayor a la distribución B cuando en realidad corresponde a la A? Lo haremos 5 de cada 100 veces, cometiendo un error alfa o tipo I (p=0.05). Ahora bien, si nos centramos en la distribución B, notamos que un valor de 1,35 mg%, correspondiente a dicha distribución, puede ser erróneamente atribuido a la distribución A, en una proporción de casos que corresponde al área rayada en verde. Es decir que existiendo una diferencia (porque 1,35 mg % corresponde a la distribución de personas enfermas, y por lo tanto cabe rechazar la hipótesis nula de no diferencia con el valor de 1 mg% que corresponde a las sanas) el test podría no ser capaz de reconocerla, cometiendo un error beta o tipo II.

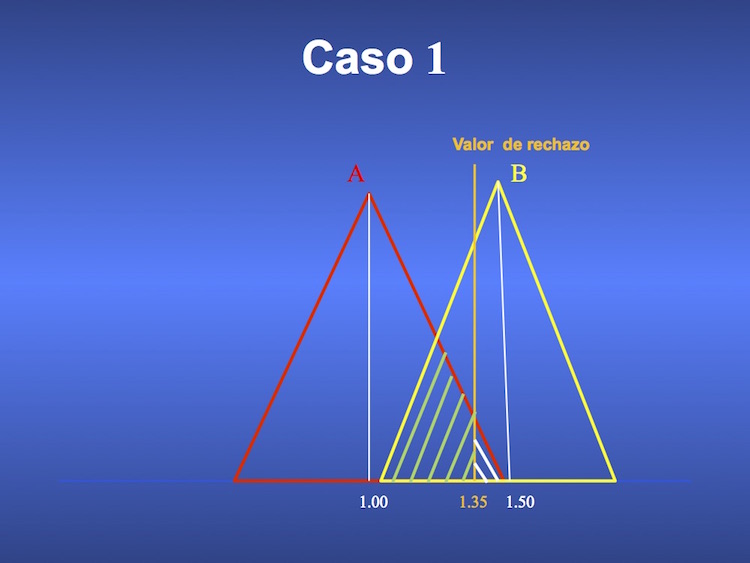
¿Qué sucede si el valor de rechazo de la hipótesis nula es menor? Las figuras 3 y 4 revelan que aumenta el error alfa (cae la especificidad), al tiempo que disminuye el error beta, y aumenta por lo tanto la sensibilidad. Error alfa y beta se mueven por lo tanto en sentido inverso. Depende del investigador si privilegia uno u otro, pero como ya dijimos, no se admite un error alfa mayor de 0.05.

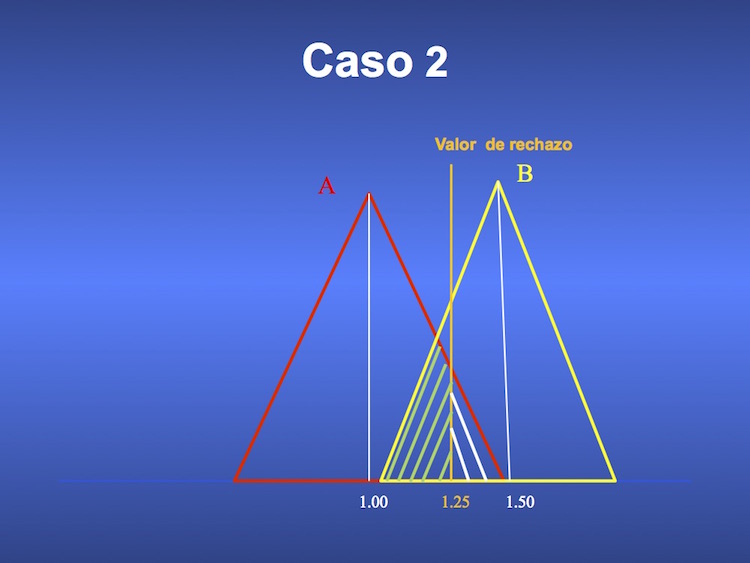
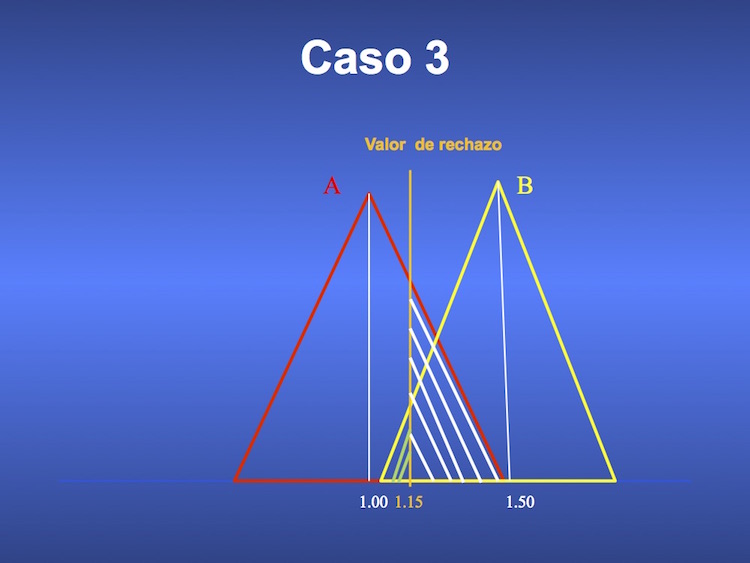
Lo veremos en una próxima entrega, pero adelantaremos que cuanto mayores la sensibilidad y la especificidad del test estadístico, y menores por lo tanto los errores alfa y beta, mayor será el número de observaciones necesarias para detectar una diferencia estadísticamente significativa.

Dr. Jorge Thierer