¿Para qué sirve la distribución muestral de medias?

En las últimas entregas hablamos de la distribución de probabilidades de datos individuales. Pero en la práctica cotidiana de la investigación no trabajamos para ubicar en una distribución los datos individuales que ya tenemos; para saber si un valor tiene alta o baja probabilidad de ocurrencia bastaría en este caso con ordenar todos los valores de menor a mayor y ver qué lugar ocupa en la distribución, cuán cercano está a la media o la mediana.

Cuando hacemos investigación nos interesa inferir si los hallazgos de un grupo de pacientes son similares a los de la población general, o a los de otro grupo, o bien si se trata de valores distintivos. Para inferir si hay o no diferencias es que resulta fundamental trabajar con la distribución muestral de medias.

Cuando en una población se toma una muestra y se mide una variable continua, se obtiene un conjunto de mediciones que puede resumirse en un valor de media. Si se toma otra muestra de la misma medición se obtendrá otra media. Puede intuirse entonces que podemos tomar infinitas muestras y obtener por lo tanto infinitas medias. Esas medias por lo tanto constituyen a su vez una variable continua, que como toda variable continua tiene determinada distribución de probabilidades.

El teorema del límite central nos dice que todas las medias de una variable se distribuyen alrededor de la media de la población: la media de todas las medias es la media poblacional. Notemos que no estamos hablando ahora de datos individuales en torno de la media de una muestra: estamos hablando de medias de muestras en torno de la media poblacional.

Y lo más interesante es que si las muestras son de tamaño suficiente (más de 30 observaciones, aunque algunos hablan de más de 100) las medias se distribuyen alrededor de la media poblacional en forma gaussiana, aún cuando la variable en la población general no tenga esa distribución! En esta curva gaussiana la medida de posición es la media poblacional. Y la medida de dispersión no es el desvío estándar, como en la distribución en una muestra, sino el error estándar de la media (SEM), que es el desvío estándar dividido por la raíz cuadrada del tamaño de la muestra:

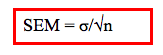
Entonces, y trabajando con los conceptos de estandarización de la distribución gaussiana y considerando que en una distribución muestral de medias

z = (media de la muestra- media de la distribución de medias)/ SEM,

obtenido el valor de z que corresponde a nuestra media podremos considerar en qué posición se encuentra respecto de la media poblacional, y cuál es la probabilidad de tener valores iguales, menores o mayores.

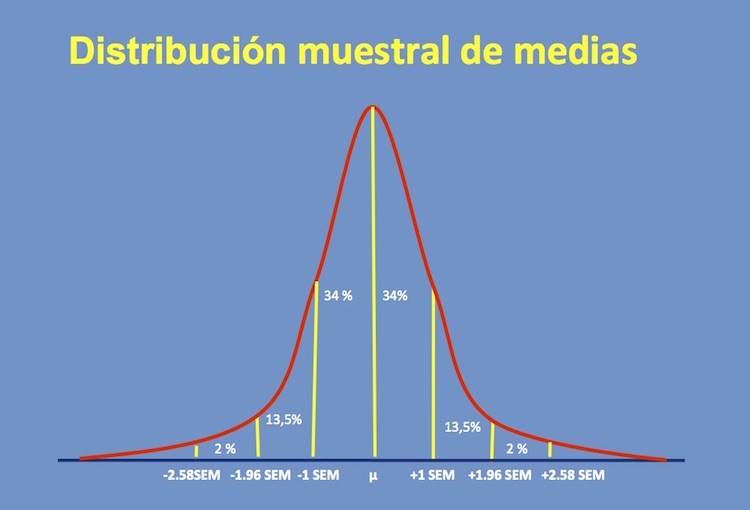
Así como en una distribución gaussiana de valores individuales entre ± 1 desvío estándar se engloba aproximadamente el 68% central de las observaciones, entre la media ± 1.96 desvíos estándar se engloba aproximadamente el 95% central y entre la media ± 2.58 desvíos estándar se engloban aproximadamente el 99% central de las observaciones, en la distribución muestral de medias entre la media poblacional ± 1, ± 1,96 y ± 2.58 SEM se engloban aproximadamente el 68%, el 95% y el 99% central de las medias (figura).

No sólo las medias tienen distribución muestral: también las proporciones, las varianzas, etc. El concepto de distribución muestral es central para comprender la lógica de los tests estadísticos, a los que nos referiremos en la próxima entrega.

Si la distribución de probabilidades de una variable continua es claramente asimétrica (media significativamente diferente de la mediana, alta dispersión de datos) no es posible calcular la probabilidad de un resultado o valor determinado; no tenemos cómo ubicarlo dentro de la distribución, porque la misma carece de parámetros. En este caso, a veces se recurre a artilugios matemáticos según el caso (elevar los datos a una potencia, sacarles la raíz cuadrada o cúbica, expresarlos con su logaritmo) para “normalizar” la distribución, transformarla en gaussiana y trabajar como acá hemos descrito.

Dr. Jorge Thierer