¿Qué es el análisis de sobrevida? Parte 4

En la comparación de 2 o más grupos o cohortes definidos por la presencia/ausencia de una variable, o por la pertenencia a una categoría determinada, representamos la evolución de cada uno en el tiempo con una curva de Kaplan Meier.

Como dijimos, podemos por ejemplo en un estudio observacional comparar la evolución de pacientes con y sin insuficiencia renal tomando como punto final sobrevida. Veremos entonces la curva de sobrevida para ambas cohortes (figura 1). Podemos también, en un estudio de intervención comparar la evolución de pacientes tratados con droga y placebo, o con dos drogas diferentes, o con diferentes procedimientos. También en este caso, veremos dos curvas de sobrevida superpuestas.

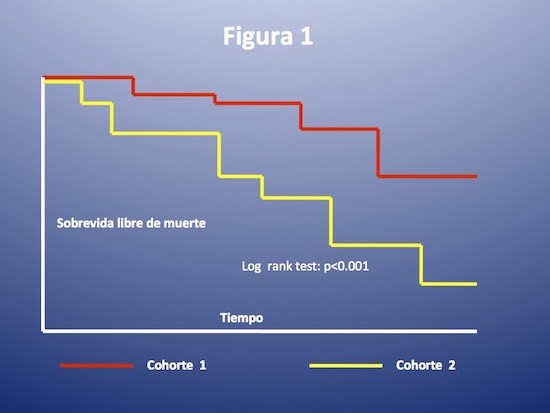
Pero, ¿cómo se establece si ambas curvas presentan diferencia estadísticamente significativa? Cómo establecer si la variable que determina la pertenencia a una u otra curva influye en la evolución?

Así como en la regresión logística la fuerza de asociación de una variable predictora con la evolución o la respuesta se expresa mediante el odds ratio (OR), en el caso del análisis de sobrevida la medida de asociación es el hazard ratio (HR). Valen para el HR las mismas consideraciones que hicimos en su momento para el RR y el OR. Recordemos los puntos esenciales:

En el caso de una variable dicotómica el HR expresa el aumento en la probabilidad de ocurrencia de un fenómeno cuando la variable predictora está presente respecto de cuando está ausente. Por ejemplo, si analizamos en una cohorte el riesgo de IAM debido a la diabetes, un HR de 2 significa que la diabetes duplica el riesgo de presentar un IAM a lo largo del seguimiento.

En el caso de una variable continua el HR expresa el aumento en la probabilidad de ocurrencia de un fenómeno cuando la variable predictora aumenta en una unidad. Por ejemplo, si en la misma cohorte analizamos el riesgo de IAM que acarrea un aumento de la hemoglobina glicosilada, un HR de 1,16 significa que el riesgo de IAM a lo largo del seguimiento aumenta un 16% por cada incremento de 1% en el valor de la misma.

Como en el caso de los RR o los OR, los HR tienen también un IC 95%. Si el extremo inferior del IC 95% es > 1, ello implica aumento del riesgo con p

En general este tipo de análisis se realiza bajo los supuestos de un modelo, el modelo de riesgos proporcionales de Cox. Este modelo considera que el riesgo (hazard) de ocurrencia del evento de cada observación tiene dos componentes: un componente vinculado al paso del tiempo, que es similar para todos los observados , y un componente vinculado a la presencia o ausencia de la/s variable/s de interés. Y se entiende, para que el modelo sea válido, que el riesgo atribuible a esa variable se mantiene más o menos constante a lo largo del tiempo, y es proporcional en un grupo respecto del otro. Volviendo al ejemplo anterior, si la diabetes duplica el riesgo de IAM, entonces cualquiera sea el riesgo de IAM en los no diabéticos a lo largo del tiempo, en los diabéticos siempre será aproximadamente el doble, con sus más y menos considerados por el IC 95%.

Si la relación de riesgo varía fuertemente a lo largo del tiempo, de manera que la relación de riesgos asociados a la variable en un momento y otro de la evolución son muy distintos, otro tipo de análisis deberá realizarse. (en la figura 2 el riesgo asociado a pertenecer a la cohorte 1 es mayor que pertenecer a la 2 hasta la mitad del seguimiento, luego la relación se invierte).

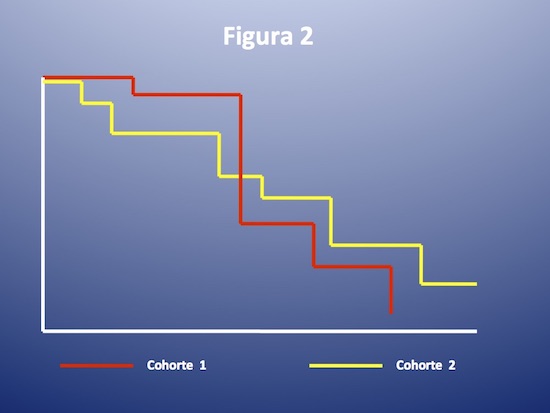
El HR cuantifica el riesgo en el tiempo asociado a la presencia de una variable. Otra forma de establecer comparación entre ambas curvas, sin cuantificar la relación de riesgo, es el log rank test, que solemos ver en el gráfico de las curvas. Veamos de qué se trata:

Bajo la hipótesis nula, si entendemos que el riesgo en ambas curvas es el mismo, cada vez que se produce un evento, podemos pensar que el mismo debería haberse repartido entre ambas. Ejemplo: tenemos 100 pacientes, 60 en el grupo 1, 40 en el grupo 2. En un momento hay una muerte en el grupo 1 (1 muerte sobre un total de 100 pacientes). Si los grupos fueran iguales al momento de producirse esa muerte en uno de los grupos, hubiéramos esperado 1/100 de muerte en el grupo 1 (1/100 de 60, 0,6) y 1/100 de muerte en el grupo 2 (1/100 de 40, 0,4). Pero en lugar de lo esperado (0,6 muertes en grupo 1, y 0,4 muertes en grupo 2) lo observado es 1 muerte en grupo 1 y ninguna en el grupo 2. Hay diferencia entre lo observado y lo esperado. Sucesivamente, cada vez que se produzca un evento en uno u otro grupo volveremos a tener una diferencia entre lo observado y lo esperado bajo la hipótesis de nulidad. En cada momento un test nos arrojará un valor estadístico que surge de comparar lo observado con lo esperado. Y al final del seguimiento tendremos un valor final de ese test, fruto de la suma de las comparaciones parciales, que corresponderá a un determinado valor de p. Si ese valor de p es < 0.05, las curvas son estadísticamente diferentes. Si el valor de p es mayor no podremos rechazar la hipótesis de nulidad (ver figura 1).

En resumen: en la comparación entre dos cohortes, el HR y su IC 95% nos informarán si hay diferencia significativa en la sobrevida y cuantificarán la asociación de la variable basal con el pronóstico. El log rank test nos dirá, sin cuantificar la asociación, si las curvas corresponden a sobrevidas significativamente diferentes.

Tres comentarios finales:

En la primera parte de Análisis de Sobrevida dijimos que el mismo emplea toda la información disponible que en el seguimiento ha aportado cada observación, hasta el momento mismo en que a) sucede el punto final, b) se pierde el contacto u ocurre otro punto final que impide la valoración del punto de interés (por ejemplo, si el punto final es disfunción renal y el paciente muere sin que hayamos podido definir si hubo o no dicho deterioro), o c) culmina el seguimiento. En cada una de estas situaciones hablamos de dato censurado, en el sentido de que entrega información hasta ese momento.

Hemos presentado en todos los ejemplos curvas de libertad de eventos. Es lógico que en estos casos las curvas son descendentes: al principio del seguimiento todos los observados están libres del evento de interés (por ejemplo, mortalidad). A medida que pasa el tiempo y los eventos ocurren, la libertad de eventos es menor. Pero las curvas de Kaplan Meier pueden ser curvas que grafiquen la ocurrencia progresiva de eventos. En este caso serán ascendentes. Por ejemplo, se inicia el seguimiento y nadie ha muerto: la incidencia del evento es 0%. A medida que se acumulen las muertes la curva irá ascendiendo (figura 3).

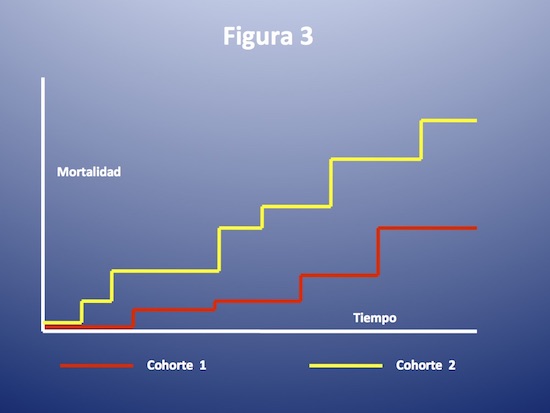
En base a lo expresado en la parte 2 de esta serie dedicada al análisis de sobrevida, siempre que se analiza una curva debemos detenernos en la cantidad de pacientes en riesgo, cuyo número aparece al pie del gráfico. Ello nos permitirá definir si los datos presentados (sobrevida libre de eventos, o incidencia de los mismos) nos resultan confiables, al tener en cuenta que el intervalo de confianza aumenta a medida que las observaciones disminuyen.

Dr. Jorge Thierer