¿Qué es el análisis multivariado? Parte 4

Recordemos nuevamente al principio algunos conceptos ya vertidos en entregas previas.

Las distintas formas de análisis multivariado a que nos hemos referido hasta ahora parten de un supuesto fundamental: entre las variables predictoras y la respuesta hay una relación lineal.

Hay relación lineal de las variables predictoras a) con la variable continua cuyo valor se está buscando predecir en la regresión lineal, b) con el logaritmo natural del odds ratio en la regresión logística, c) con el logaritmo del hazard ratio en el análisis de sobrevida.

Este supuesto vale para variables predictoras categóricas dicotómicas y para variables continuas. En el primer caso hablaremos del cambio en la respuesta cuando la variable dicotómica está presente respecto de cuando está ausente. En el segundo, de cuánto cambia la respuesta por cada cambio en una unidad en la variable continua.

Pero hay casos en que no podemos hablar de relación lineal. ¿Cómo proceden los autores en casos así? Veremos ejemplos y la forma de resolverlos.

1. La variable predictora es nominal, pero con más de 2 categorías, o es una variable ordinal.

Supongamos que estamos explorando la relación entre la ausencia o presencia de insuficiencia mitral (y en este caso su severidad) con la mortalidad en el seguimiento. Insuficiencia mitral es en este caso una variable categórica, que puede asumir los siguientes valores: no, leve, moderada, severa. Vamos a expresar la asociación de estas categorías con el resultado muerte, empleando como medida de asociación el OR. ¿Cómo se expresa entonces esa asociación de 4 categorías diferentes de una sola variable, con un resultado? Mediante la creación de variables dicotómicas múltiples o dummy.

Tendremos entonces una variable IM no (definida como 1 si no hay IM y 0 si hay algún grado de IM); una variable IM leve, una variable IM moderada y una variable IM severa (en cada caso con valor 1 si están presentes y 0 si no lo están). Cuatro variables dicotómicas que expresan una de las cuatro categorías de la variable primigenia IM. ¿Pero son necesarias las cuatro? Veamos la tabla 1 parte superior. Notemos que para el programa de computación si en una observación las variables IM leve, moderada y severa asumen valor de 0, por fuerza debe tratarse de una observación que corresponde a IM no (ver tabla 1 parte inferior). De allí que el número de variables dummy consideradas en un análisis es igual al número de categorías de la variable original menos 1.

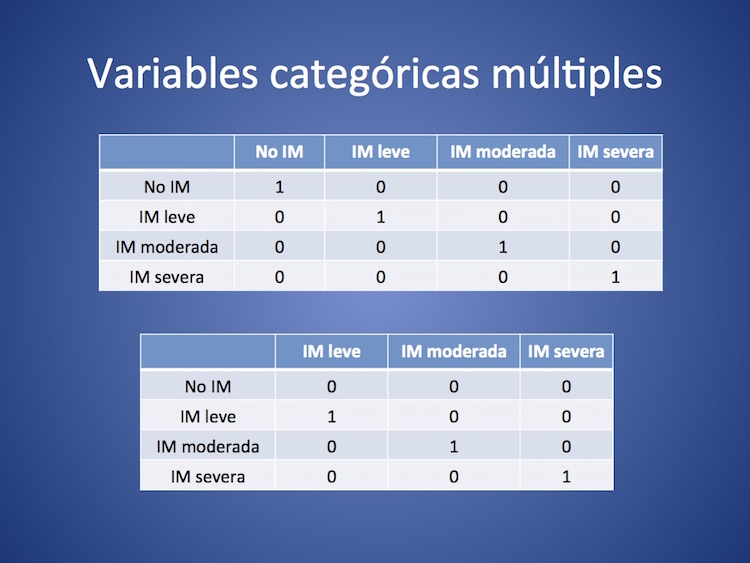
La variable dummy excluida funciona como referente. No siempre es como en nuestro ejemplo la que se define por corresponder a un valor 0 en todas las otras de la familia. A veces se define como referente a la que tiene menor asociación con la variable respuesta, o el programa elige excluir a la que tiene mayor cantidad de observaciones, etc.

La ventaja del empleo de variables dummy es que permite incorporar al análisis variables nominales con varias categorías o variables ordinales. La desventaja es que aumenta el número de variables incorporadas, haciendo más difícil cumplir con las reglas que mencionamos en la entrega anterior acerca del número ideal de variables en el análisis.

2. La variable predictora es continua, pero la relación con el evento no es lineal.

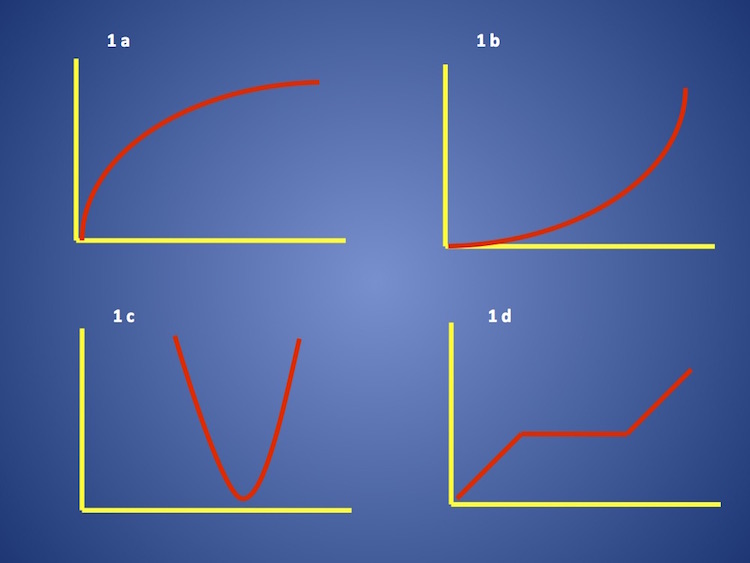
Pueden darse diferentes relaciones de la variable predictora con la respuesta, claramente no lineales. Veamos ejemplos en las figuras 2 a, b, c y d. En cada una de ellas graficamos en abscisas la variable predictora y en ordenadas la variable respuesta.

En la figura 1 a vemos que con escaso incremento inicial de la variable predictora hay gran aumento de la incidencia de la variable respuesta. Pero para conseguir un aumento similar hace falta luego un aumento mucho mayor de la variable predictora. La relación de la variable predictora con el evento no es lineal.

¿Qué pasa si hacemos una transformación logarítmica de la variable predictora? Por ejemplo, una variable como NT pro BNP asume valores que pueden ir de menos de 100 a más de 35.000 pg/ml. Su relación con mortalidad asume una distribución como la que muestra la figura 2 a. No es una relación lineal. Pero si trabajamos con logaritmos en base 10, todos los valores entre 10 y 100 tienen un valor que comienza con 1; entre 100 y 1.000 un logaritmo que comienza con 2; entre 1.000 y 10.000, con 3 y así sucesivamente. Trabajar con el logaritmo de NT pro BNP lineariza la relación con el evento. Un efecto similar puede lograrse si en vez de trabajar con logaritmos decimales lo hacemos con los logaritmos naturales de base e, los mismos que vimos al explicar regresión logística.

En la figura 1 b encontramos una relación no lineal entre una variable continua y el evento, antitética a la anterior. En este caso el aumento en la respuesta es más notable en el rango de valores altos de la variable predictora. A diferencia del ejemplo anterior, hay que hacer en este caso una transformación antilogarítmica, elevando e o 10 al valor de la variable continua.

En la figura 1 c vemos una relación en U: valores bajos y altos de la variable predictora se asocian a la misma respuesta. Pensemos por ejemplo en la relación entre colesterol plasmático y mortalidad. No hay relación lineal entre predictor y evento. ¿Cómo proceder? Se puede recurrir a incluir en el análisis un término cuadrático, que surge de restar en cada caso al valor individual de la variable el valor de la media y elevar esa diferencia al cuadrado. A valores bajos y altos equidistantes de la media y con la misma relación con la variable respuesta (por tratarse de una curva en U) corresponderá el mismo término cuadrático, y de esa manera se conseguirá hacer lineal la relación. Supongamos que en la relación de colesterol con mortalidad, las cifras más bajas de la misma corresponden a un valor de colesterol de 150 mg/dl, que corresponde a la media de las observaciones. Y que valores de 100 mg/dl y de 200 mg/dl se asocian a una mortalidad más alta, y similar en ambos casos. Si se introduce un término cuadrático, entonces X menos la media corresponde a un valor cuadrático:

Para 150 de 0, porque (X- media)² = (150 – 150)²= 0 2 = 0
Para 100 de 2.500, porque (X- media)² = (100 – 150)²= (-50)² = 2.500
Y para 200 también de 2.500, porque (X- media)² = (200 – 150)²= (50)² = 2.500

De esta manera se lineariza la relación con el evento en una curva en U o en una curva en J, que funciona de la misma manera. Pero puede recurrirse también a la creación de variables dummy, estableciendo categorías de la variable predictora (por ejemplo, colesterol entre 75 y 125 mg/dl, 125 y 175 mg/dl, 175 y 225 mg/dl) y elegir como categoría referente a la que incluye la media, valorando entonces la asociación de las otras categorías respecto de la primera con la mortalidad.

En la figura 1 d vemos una relación en la que puede plantearse la existencia de un umbral. El incremento en los valores de la variable predictora se asocia inicialmente a un aumento del riesgo. Alcanzado un valor determinado se estabiliza el riesgo, y así mientras aumenta la variable predictora hasta que se alcanza un nuevo valor que supone en adelante un incremento del riesgo. Nuevamente se puede recurrir a la creación de variables dummy, tomando como referente el valor umbral.

En la próxima entrega terminaremos de explorar algunos aspectos fundamentales del análisis multivariado.

Dr. Jorge Thierer