¿Qué es el intervalo de confianza del 95%? ¿Para qué sirve? Parte 1

Vamos inicialmente a recordar algunos conceptos de entregas previas.

Las variables con las que trabajamos a diario son aleatorias, es decir que pueden asumir valores diferentes. Para cada tipo de variable hay medidas que condensan o resumen el valor de un conjunto de observaciones en uno solo. Si la variable es categórica un conjunto de observaciones se resumirá en un porcentaje; si es continua en una media o mediana. La variabilidad (de allí que sean variables, justamente) o dispersión de los datos se expresará en medidas en términos de desvío estándar cuando hablamos de una muestra de un conjunto de individuos, y de error estándar cuando nos referimos a un conjunto de medias o proporciones.

Por ejemplo, en una muestra de 400 individuos de una población, el valor de colesterol se expresa por una media de 168 mg/dl, con un desvío estándar de 40 mg/dl. ¿Es esta media una buena estimación de la media de la población? ¿Cuál será el valor de la media poblacional?

De acuerdo con el teorema del límite central todas las medias que surgen de diferentes muestras con igual n o número de observaciones de una población se distribuyen en torno de la media poblacional en forma gaussiana, con una dispersión expresada por el error estándar (SEM). El SEM es el desvío estándar dividido por la raíz cuadrada del número de observaciones,

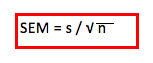
y entre la media ± 1,96 SEM se encuentra el 95% de las medias que podrían obtenerse en esa población con muestras de igual n.

En el ejemplo el SEM es 20/√ 400= 40/20=2. Por lo tanto, entre 168 – (1,96 x 2) y 168 + (1,96 x 2), o sea entre 164,08 mg/dl y 171, 92 mg/dl podemos esperar que se encuentre la media poblacional el 95% de las veces.

El intervalo de confianza de 95% (IC 95%) de nuestra medición se mueve entonces respecto de la media poblacional entre 164,08 y 171,92. Confiamos en que si repitiéramos el experimento 100 veces, tomando 100 muestras de n=400, 95 veces la media de colesterol estaría comprendida entre los valores citados, a los que denominamos extremos del intervalo de confianza.

El intervalo de confianza expresa entonces cuán confiable es nuestra estimación. Decimos que la media de colesterol es 168, pero en esta población 95 de cada 100 muestras podrían haber tenido medias con valores que oscilaran prácticamente entre 164 y 172.

¿Qué hubiera pasado si en iguales condiciones, con igual n y la misma media, el desvío estándar hubiera sido 80 mg/dl en vez de 40 mg/dl? El SEM sería 4, y los extremos del IC 95% hubieran sido 160,16 y 175,84. Es decir, que con un desvío estándar mayor el IC 95% es más amplio. ¿Y si el desvío estándar hubiera sido solo 20 mg/dl? El SEM sería 1, y los extremos del IC 95% hubieran sido 166,04 y 169,96. Con un desvío estándar menor el IC 95% es más estrecho.

¿Qué hubiera pasado si los valores hallados (media de 168 mg/dl y desvío estándar de 40 mg/dl) provinieran de una muestra no de 400 sino de 1.600 individuos? Haciendo las cuentas, el SEM sería 1, y el IC 95% nuevamente estaría entre 166,04 y 169,96. Con n mayor, el IC 95% es más estrecho. ¿Y si la muestra fuera de solo 100 observaciones? El SEM sería 4, y el IC 95% estaría entre 160,16 y 175,84. Con n menor, el IC 95% es más ancho.

El concepto de intervalo de confianza se vincula con el de la precisión de la estimación. Cuanto más estrecho el intervalo, más confiable es nuestra estimación. Como vemos, ello se consigue con menor dispersión de datos, o con mayor número de observaciones.

En la próxima entrega profundizaremos en el concepto de intervalo de confianza y veremos otras aplicaciones.

Dr. Jorge Thierer