¿Qué es el propensity score? Parte 2

En la entrega anterior comenzamos a desarrollar el tema del empleo de los propensity scores. Recordemos los conceptos fundamentales, que ya desarrollamos en detalle a lo largo de diferentes secciones:

Cuando se decide llevar a cabo una intervención o no hacerlo, hay factores que están asociados estadísticamente con tomar esa decisión. Si comparamos entonces una intervención con otra, o realizarla con no hacerlo, es difícil poder adjudicar con certeza el resultado y la evolución alejada exclusivamente a la conducta tomada, porque dicho resultado puede estar determinado en parte o totalmente por las condiciones basales que llevaron a elegir una conducta u otra. Las variables basales, si se vinculan estadísticamente con la elección de la conducta, y además se vinculan estadísticamente con la evolución alejada, son confundidoras de la relación entre la intervención y el resultado.

Los estudios aleatorizados, al adjudicar al azar la intervención, eliminan el sesgo de selección presente al elegir una conducta en base a las características de base. De manera entonces, que asegurando una distribución similar de las variables basales conocidas y desconocidas, el estudio aleatorizado permite adjudicar el resultado obtenido exclusivamente a la intervención, y ese es su más importante mérito.

Pero no todas las intervenciones son probadas en estudios aleatorizados, o los mismos muchas veces no reúnen las condiciones necesarias para ser juzgados de buena calidad. En realidad, solo una muy baja proporción de las medidas que tomamos a diario están respaldadas por estudios de esta índole.

Frente a esta situación se alzan los estudios observacionales, más representativos del mundo real, pero al mismo tiempo, sujetos cuando se trata de comparar intervenciones, al sesgo de selección citado.

Como una forma de reparar la falta de estudios aleatorizados en la mayor parte de los casos, y también de comparar, cuando existen, los resultados de los estudios randomizados, tan limitados en su validez externa por los criterios de inclusión y exclusión y el sesgo de participación con los del mundo real, es que surge la idea de hacer estudios que consideren el empleo de propensity scores, o puntajes de propensión.

Vimos en la entrega anterior el primer paso en la confección de los mismos. Definiendo en un estudio observacional por regresión logística simple en una población cuáles son las variables significativamente asociadas en análisis bivariado a llevar a cabo una intervención, puede luego definirse en análisis multivariado (regresión logística múltiple) cuáles son las independientemente asociadas a esa conducta. Y esas variables, predictoras independientes de llevar a cabo la intervención, pueden emplearse en la confección de un score o regla de predicción. ¿Qué predice el score? Señala la probabilidad de que cada individuo haya sido sometido a la intervención, señala la propensión a recibir la intervención. De manera que cada individuo tiene un puntaje de propensión a dicha intervención. Puntajes altos señalan alta propensión, y por lo tanto mayor probabilidad de haber recibido la intervención, puntajes bajos la condición opuesta.

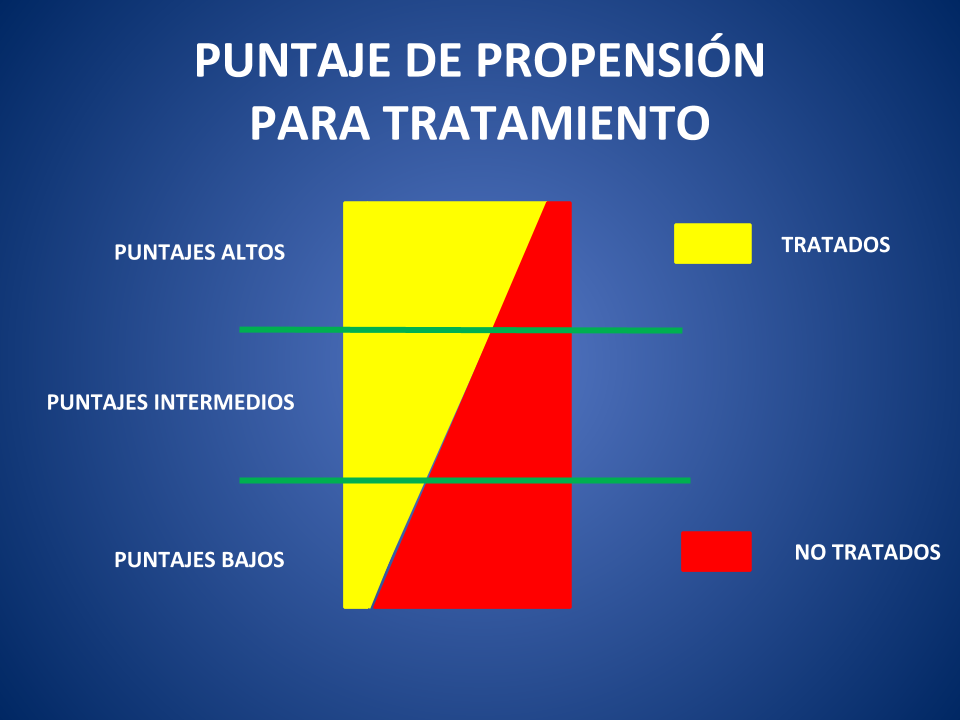
Pero una cosa es la propensión, y otra que la intervención se haya llevado a cabo efectivamente. No todos las personas con alto puntaje están efectivamente tratadas, ni todas aquellas con puntaje bajo no lo están. Podemos entonces suponer que entre aquellos con puntaje alto habrá muchos tratados y algunos no; que entre aquellas con puntajes bajos habrá alto predominio de no tratados, pero algunos sí; y que con puntajes intermedios tenderá a ser más similar la proporción de tratados y no tratados.

Figura 1

¿Cómo continuamos? Una vez que cada paciente tiene su score de propensión, el paso siguiente consiste en aparear, para cada puntaje del score, un paciente efectivamente tratado y uno no tratado. Como más allá de la propensión a estar tratado (cuantificada por el score), el tratamiento puede estar efectivamente instituido o no, lo que se busca es comparar pacientes, que teniendo igual propensión hayan sido o no tratados. La lógica imperante es que si la propensión a estar tratado es la misma, cualquier diferencia en la evolución alejada debería atribuirse al tratamiento en sí, y no a las características basales.

De manera entonces que mediante programas de estadística con comandos determinados, se aparea a cada paciente tratado con un puntaje determinado a uno de puntaje similar o lo más próximo posible (en el orden del diezmilésimo o más). Finalmente quedan definidas 2 cohortes con un score de propensión similar, y donde incluso se pueden establecer categorías del score (puntajes muy altos, altos, intermedios, etc.) y demostrar que dentro de cada categoría también los puntajes son similares entre ambas cohortes.

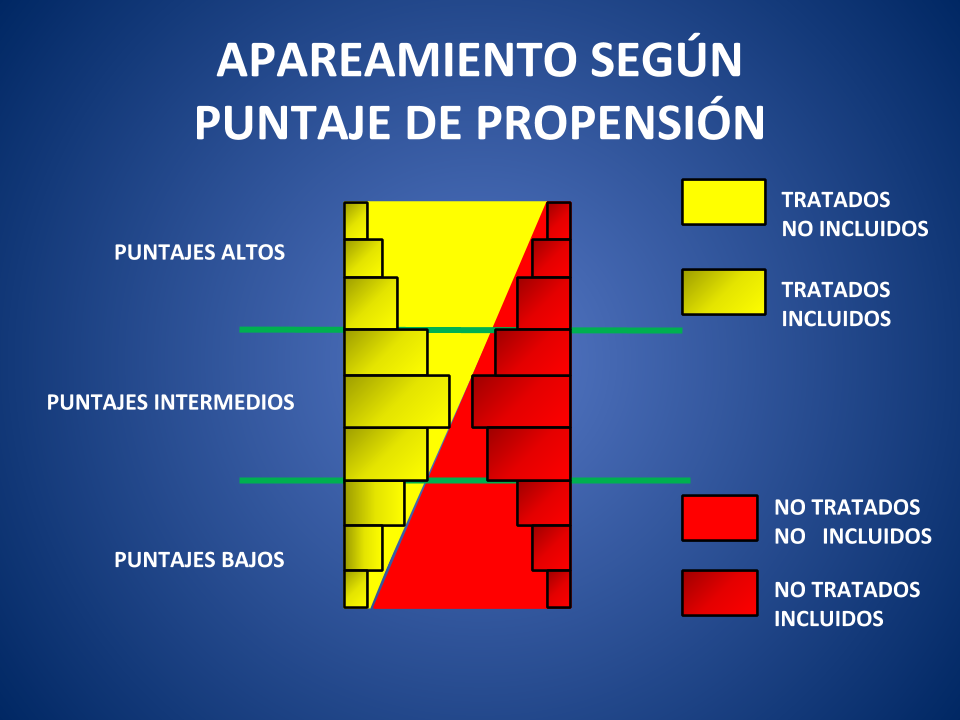
Como muestra la Figura 1, entre los pacientes con puntajes altos la mayoría está tratada y lo opuesto sucede con puntajes bajos. La Figura 2 revela que a la hora de proceder, es claro que unos pocos pacientes tratados con puntajes altos se aparean con los pocos no tratados que tienen dichos puntajes. El resto de los tratados con puntaje alto quedan fuera de la comparación, porque no tienen con quién aparearse. Y, especularmente, entre los pacientes con puntajes bajos, unos pocos no tratados se aparean con los pocos tratados disponibles. De manera que el grueso de los no tratados con puntajes bajos queda también afuera.

Figura 2

En cambio, entre los pacientes con puntajes intermedios, es mayor la capacidad de formar pares de pacientes, y la pérdida es entonces proporcionalmente menor.

Finalmente hemos logrado 2 cohortes con igual probabilidad de estar tratada (con participantes desde baja hasta alta propensión), de las cuales una lo está efectivamente y la otra no. Como si se tratara de un estudio aleatorizado, en que inicialmente cada participante puede o no recibir la intervención, y es el azar el que decide.

Pero…. ¿Es lo mismo asignar aleatoriamente un intervención que definir en un estudio observacional la propensión a recibir un tratamiento y luego aparear por dicha propensión a pacientes con el tratamiento fue efectivamente implementado o no?

No lo es. Porque una impronta fundamental de los estudios aleatorizados es que la distribución al azar reparte por igual las características basales conocidas y las desconocidas. Más allá de lo que vemos o los datos que recabamos puede haber variables que no conocemos y que sean las verdaderas responsables de la diferente evolución de 2 cohortes, confundidores no tenidos en cuenta. La aleatorización asegura razonablemente que incluso esas características desconocidas están igualmente distribuidas en tratados y no tratados. En cambio, el score de propensión se construye post hoc, en base solo a las características conocidas que fueron consideradas a la hora de recabar la información. No podemos afirmar que no haya características desigualmente repartidas en las que no reparamos, que se relacionen con la evolución, esto es, confundidores no considerados, lo que se llama confusión residual.

Y a esto debemos agregar que, como vimos, pacientes en los extremos del puntaje contribuyen poco a la comparación porque no tienen contraparte con la que aparearse. Gran parte de la información ofrecida por el alto número inicial de pacientes se pierde en aras de aparear y simular un estudio aleatorizado

En la próxima entrega concluiremos con el tema, veremos si hay alternativas al apareamiento cuando empleamos el score de propensión y qué otras utilidades pueden dársele.

Dr. Jorge Thierer