¿Qué es la distribución normal o gaussiana?

En la entrega anterior nos referimos al concepto usual de probabilidad y a las distribuciones binomial y de Poisson. Vamos a hablar ahora de la distribución de probabilidades en el caso de variables cuantitativas continuas, las que usamos más frecuentemente en medicina. Por ejemplo, los datos antropométricos, las mediciones de laboratorio, las determinaciones ecocardiográficas, etc. La información en este caso se expresa como media y desvío estándar o como mediana y rango intercuartilo. Si la media y la mediana son similares, y el desvío estándar es un 20 a 30% del valor de la media podemos suponer que la distribución de los datos es normal o gaussiana.

La distribución normal o gaussiana (figura 1) es acampanada, simétrica, unimodal, con media y mediana similares y las colas cercanas a 0. La ventaja de la distribución gaussiana es que permite inferir la probabilidad de que se presente determinado valor y los mayores o menores que él. Ello se debe a que tiene parámetros, valores que nos permiten ubicarnos dentro de la distribución. Dichos parámetros son la media y el desvío estándar. Sabemos que la media ocupa el lugar central de la distribución, y que la media ± 1 desvío estándar engloban aproximadamente el 68% central de las observaciones, que la media ± 1.96 desvíos estándar engloban aproximadamente el 95% central y que la media ± 2.58 desvíos estándar engloban aproximadamente el 99% central de las observaciones. Que la distribución sea paramétrica permite entonces ubicar la probabilidad de que se dé determinado valor en la distribución.

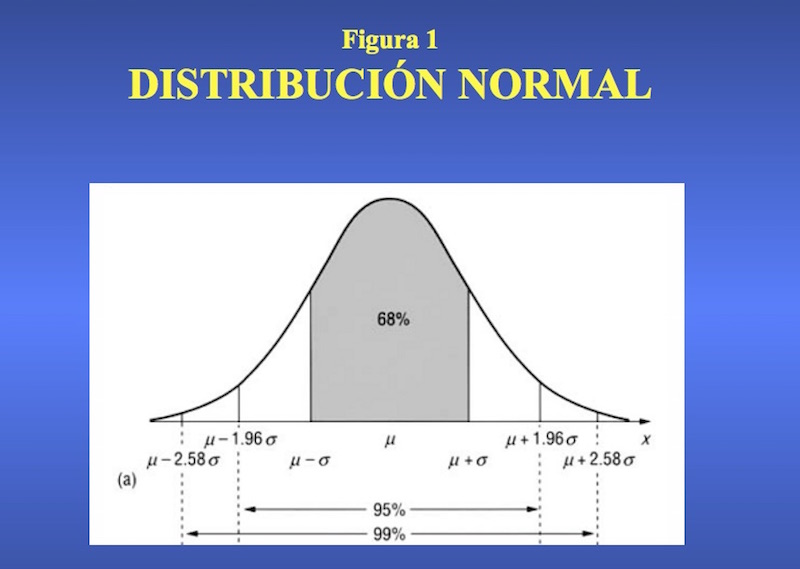
Por ejemplo: si en 120 determinaciones de hematocrito la media es 40 y el desvío estándar es 6, ¿cuál es la probabilidad de tener en esa distribución un valor de 51,76 o mayor? El valor de 51,76 está a una distancia de 1,96 desvíos estándar de la media de 40: (51,76 – 40) / 6 = 11,76/6=1,96. Dijimos que la media ± 1,96 desvíos estándar engloba el 95% central de las observaciones, por lo que por fuera (valores más allá de los 1,96 desvíos estándar hacia uno u otro lado) queda el 5 % restante. Si la distribución es simétrica, hay un 2,5% de valores mayores que la media + 1,96 desvíos estándar y un 2,5% de valores menores que la media – 1,96 desvíos estándar. Entonces, la probabilidad de tener un valor de 51,76 o mayor es de 2,5%.

Ahora bien, para cada variable continua existe infinita cantidad de distribuciones gaussianas posibles, con diferentes valores de media y desvíos estándar. Con el mismo valor de media, la distribución y por ende la forma de la curva será diferente al variar el desvío estándar. Y estamos hablando de un solo valor de media. Imaginemos la cantidad de curvas posibles si además cambia el valor de la misma. Aparece entonces un problema: ¿cómo comparar 2 distribuciones de la misma variable, y cómo decidir si un valor de una distribución es más extremo que un valor de otra?

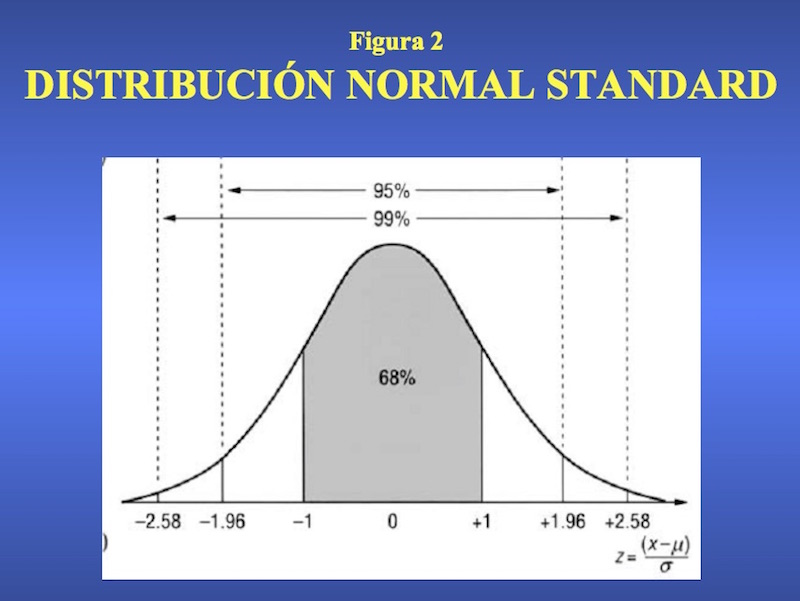
La respuesta a este problema es la distribución normal estándar (figura 2). Es una curva gaussiana en la que la media vale 0, y el desvío estándar vale 1. De manera que en esta curva entre + y -1 se engloba el 68 % de las observaciones, etc. La distancia del valor de cualquier medición a la media de la distribución se expresa en términos de z. ¿Qué es z? El valor que surge de restar el valor de la media al de dicha medición, y dividirlo por el desvío estándar de la distribución. En el ejemplo del hematocrito, un valor de 46 corresponde a 1 valor de z de + 1, y un valor de 34 a un valor de z de – 1. Z es finalmente a cuántos desvíos estándar se encuentra una medición determinada de la media de la distribución respectiva. Por eso hablamos de una distribución estandarizada: trátese de una curva de valores de colesterol, espesor septal, edad, altura, índice de masa corporal o la variable cuantitativa que sea, siempre podemos estandarizarla, y decir a qué valor de z corresponde en esa curva (con media y desvío estándar determinados) una medición cualquiera. Ese valor de z nos marca en la curva la ubicación, y por lo tanto la probabilidad de tener en la distribución un valor similar o mayor, o similar o menor.

Dr. Jorge Thierer