¿Qué es la interacción?

Recientemente incorporamos el concepto de confundidor. Recordemos que llamamos así a una variable que en la relación entre la variable predictora y variable resultado o evento está estadísticamente asociada a ambas. La fuerza o la dirección de la asociación entre predictora y respuesta está modificada por la presencia del confundidor.

Vamos a referirnos ahora a un concepto que algunos emparentan con el de confundidor, pero que es claramente diferente: el de interacción o modificación de efecto.

Decimos que hay interacción o modificación de efecto cuando el efecto de la variable predictora sobre la variable respuesta difiere en diferentes estratos de una tercera variable. La variable modificadora de efecto puede ser cualitativa o cuantitativa. A efectos didácticos vamos a centrarnos en una de tipo cualitativo dicotómico.

Veamos un ejemplo (Tabla 1). Supongamos una variable predictora A y una variable respuesta B. Cuando A está ausente la incidencia de B es 2%. Cuando A está presente la incidencia de B es 6%. Podemos decir entonces, recordando conceptos anteriores que el riesgo relativo de que B ocurra cuando A está presente respecto de cuando está ausente es 3.

Consideremos ahora la presencia de una tercera variable, M. (Tabla 2). Hay pacientes con M presente en los que además está presente A, y otros en los que A está ausente. De igual modo, entre aquellos con M ausente, A está presente en algunos sí y en otros no.

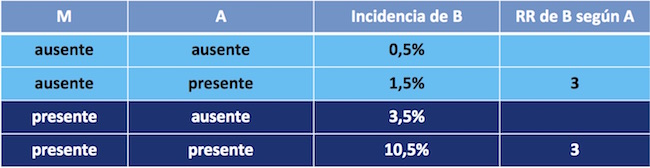
Vemos que cuando M está ausente el RR para B en presencia de A es 3 (1,5%/0,5%), y cuando M está presente el RR para B en presencia de A sigue siendo 3 (10,5%/3,5%). Es cierto, la presencia de M se asocia a mayor incidencia de B. Pero el RR de B respecto de A sigue siendo el mismo. Esto significa que no hay modificación del efecto de A sobre B, según que M esté presente o ausente. Por lo tanto, A no interacciona con M.

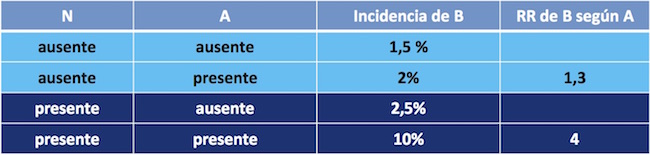
Pero veamos qué sucede si consideramos otra variable, N (Tabla 3). En este caso, cuando N está ausente, el RR para B en presencia de A es 1,3 (2%/1,5%); cuando N está presente el RR para B en presencia de A es 4 (10%/2,5%). Esto significa que el efecto de A sobre B es diferente en los diferentes estratos (presente/ausente) de N. Por lo tanto en este caso sí hay interacción de A con N.

La interacción de 2 o más variables sobre una tercera puede estudiarse en modelos aditivos o multiplicativos.

En un modelo aditivo nos planteamos si el número de casos atribuible a la presencia conjunta de A y N es igual a la suma de los casos que podemos esperar por separado debido a la presencia de A y a la presencia de N. Si el número de casos es significativamente mayor o menor que el esperable por la suma de los efectos aislados de A y N, hay interacción de A y N.

En un modelo multiplicativo (el que empleamos en las tablas que nos sirvieron de ejemplo) nos planteamos si el efecto (evaluado por ejemplo por RR u OR) atribuible a la presencia conjunta de A y N es igual al producto de los efectos que podemos esperar por separado debido a la presencia de A y a la presencia de N. Cuando no hay interacción entre las 2 variables predictoras, el efecto conjunto de ambas sobre la variable respuesta es igual al producto de los efectos individuales. Por ejemplo, si para la ocurrencia de B la presencia de A implica un RR de 2, y la presencia de N un RR de 3, el efecto conjunto de la presencia de A y N debe implicar un RR de 6.

Cuando las variables interaccionan, el efecto conjunto es mayor (interacción positiva) o menor (interacción negativa) que el esperado.

La búsqueda de interacción es característica del análisis de subgrupos en cualquier estudio de tratamiento. Por ejemplo, si una droga (variable predictora) disminuye la mortalidad (variable respuesta) ¿lo hace de igual modo en diferentes estratos de la variable edad (mayores o menores de 65 años), fracción de eyección (mayor o menor de 40%), diabetes (sí, no), etc.? La pregunta, formulada de otro modo es: hay interacción del efecto de la droga con cada una de las variables consideradas? De igual modo, en un estudio de cohorte se explora la interacción de 2 o más variables basales sobre la evolución.

Una aclaración importante: es claro que en diferentes estratos de una variable N, el RR o el OR que vincula A con B no será exactamente igual. Hay factores biológicos, variabilidad inherente a la medición, etc. Como vimos en su momento, cada OR o RR tiene un IC 95%, y pueden darse las distintas situaciones a las que nos referimos en el capítulo respectivo. Sugerimos repasarlo. Por eso, no alcanza con que los RR u OR en los diferentes estratos difieran: hay tests específicos para definir si la interacción es estadísticamente significativa.

En la próxima entrega redondearemos conceptos sobre la diferencia entre confusión e interacción.

Dr. Jorge Thierer