¿Qué es la regresión lineal?

En general los artículos que leemos se refieren a puntos finales clínicos, presentados en forma dicotómica: muerte sí/no, internación sí/no, etc. En ese caso, la asociación de los predictores con el evento se presenta como riesgo relativo, odds ratio o hazard ratio.

Pero puede ser que en el curso de un estudio se busque encontrar la asociación de variables basales con una variable respuesta numérica continua, no una dicotómica. Por ejemplo, buscar qué variables se relacionan con el incremento de la masa ventricular medida en g/m2.

Para poder realizar este análisis será necesario demostrar que ante la variación en la variable predictora hay un aumento o disminución lineal de la variable respuesta. Este punto es crucial: el cambio tiene que ser lineal, rectilíneo. Debe haber correlación (ver la entrega sobre el tema).

Es decir, que al aumentar los valores de una de ellas habrá un aumento o decremento proporcional de la otra. Es fácil inferir que de existir una relación lineal se podrá predecir aproximadamente el valor de una de las variables ante una variación de la otra. De no ser así no podría predecirse el cambio en la variable respuesta ante la variación en la variable predictora.

La relación entre la variable predictora y la respuesta se define en este caso por la ecuación de la recta (ver figura).

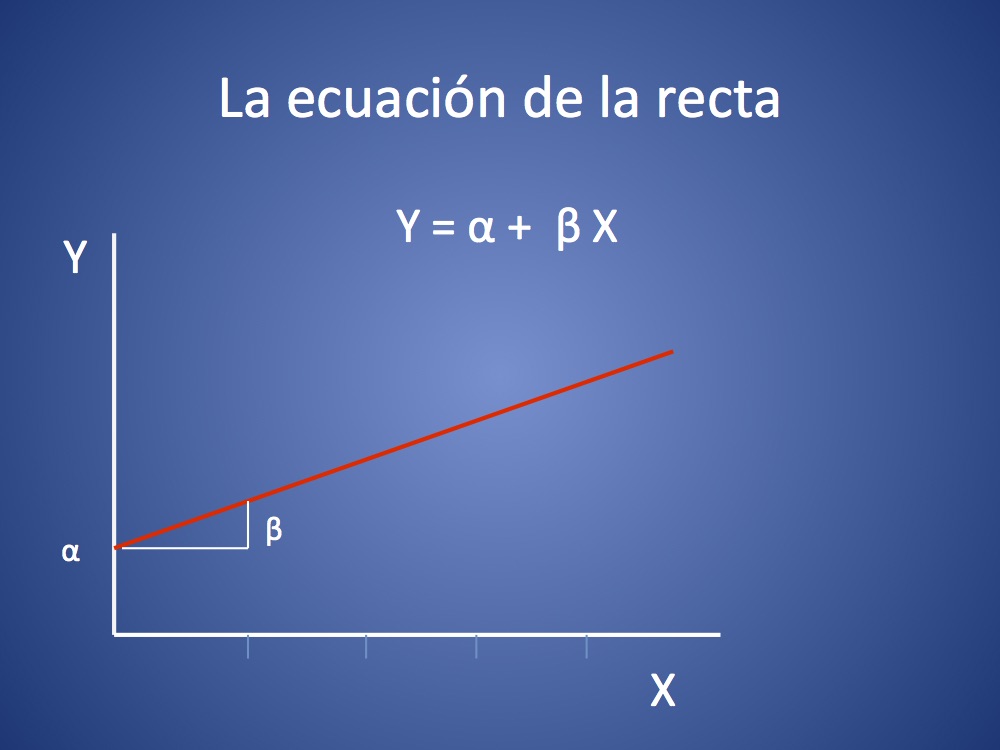
Y= α + β X
Donde:
Y es el valor de la variable continua respuesta
X es el valor de la variable predictora
α es el valor de Y cuando X vale 0
β es cuánto varía Y por cada cambio de valor de una unidad en X (ver figura)

Debe tenerse en cuenta que el hecho de que X valga 0 es teórico. Por ejemplo, si evaluamos el efecto de la edad (X) sobre la tensión arterial sistólica (Y), es claro que X no puede ser 0. Si la línea de regresión se prolongara hasta el eje de las ordenadas, X valdría 0, e Y sería igual a α.

Si X es una variable continua, β expresa cuánto varía Y (aumentando o disminuyendo) al variar X en una unidad. Por ejemplo, si en una regresión lineal que vincula hemoglobina (X) con caminata de 6 minutos (Y), decimos que

Y= 14 + 19 X

ello se lee como que si la hemoglobina fuera 0, la caminata sería de solo 14 metros (porque 19 x 0=0), y que por cada gramo que aumenta la hemoglobina, la caminata aumentará 19 metros. Si la hemoglobina fuera 10 g/dl, la caminata esperada es

14 + (19×10)= 14+190= 204 mts.

Si X es una variable dicotómica, asumiendo valor de 1 cuando está presente y 0 cuando está ausente, β expresa cuánto varía Y ante el pasaje de X de ausente a presente. Por ejemplo, si en una regresión lineal que vincula diabetes (X) con caminata de 6 minutos (Y), decimos que

Y = 309 – 77 X

ello significa que en una población de diabéticos (X=1) la caminata será
309 -( 77 x1)= 309 -77= 232 mts.

y en una de no diabéticos la caminata será
309 -( 77 x0)= 309 – 0 = 309 mts.

El valor de β surge tras realizar un procedimiento estadístico llamado regresión lineal. Un test estadístico permite definir si el valor de β es estadísticamente significativo, es decir si se aleja significativamente de 0.

Si así no fuera, entonces entenderíamos que la variación en X no impone un cambio claro en el valor de Y, porque si β vale 0, β X=0 y entonces Y= α.

En cambio, si el valor de β es significativamente diferente de 0, entendemos que hay un relación lineal entre X e Y, y que por lo tanto los cambios en X condicionan en parte los cambios en Y.

La regresión lineal que establece el valor de β para cada predictor en forma aislada se llama regresión lineal simple. Veremos más adelante el concepto de multivariabilidad y el rol que cabe a la regresión lineal múltiple.

Dr. Jorge Thierer