¿Qué es la regresión logística? Parte 2

Repasemos algunos conceptos:

Cuando se pretende definir el valor de una variable continua Y (por ejemplo, tensión arterial, filtrado glomerular, glucemia) a partir de una variable predictora X, y si la relación entre ambas variables es lineal recurrimos a la regresión lineal (ver «¿Qué es la regresión lineal?«). La relación entre la variable predictora y la respuesta se define en este caso por la ecuación de la recta (ver figura1).

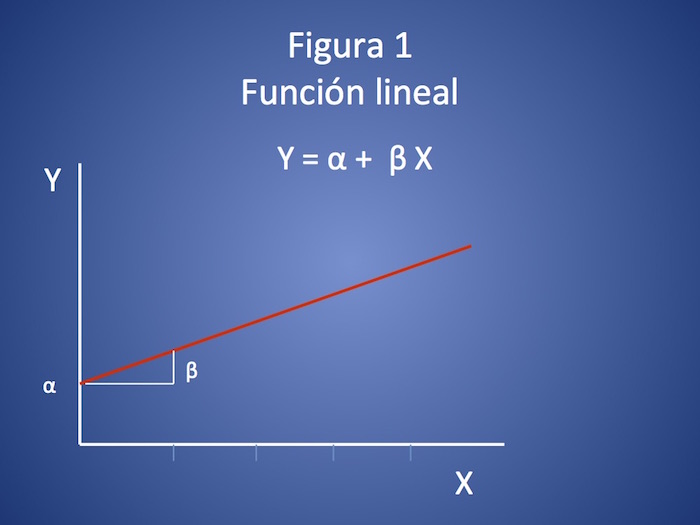
Y= α + β X

Donde:

Y es el valor de la variable continua respuesta
X es el valor de la variable predictora
α es el valor de Y cuando X vale 0
β es cuánto varía Y por cada cambio de valor de una unidad en X.

Cuando en cambio lo que buscamos es predecir la probabilidad de ocurrencia de una variable dicotómica que se define por sí/no, presencia/ausencia (por ejemplo mortalidad, internación, presencia de hipertrofia en el ecocardiograma, etc.) la regresión lineal no sirve, porque nos va a entregar valores de probabilidad que pueden ser mayores que 1 o menores que 0. Para llegar a un resultado satisfactorio tendremos que recorrer un camino que parece intrincado, pero que podremos sortear satisfactoriamente si vamos despacio.

Como la función lineal no es adecuada recurriremos a otra función matemática, la función logística (ver figura 2). Como podemos notar, esta función se grafica con una curva en forma de S itálica, que en sus extremos progresa muy lentamente y lo hace más rápido en la parte central. Un dato esencial es que la función logística entrega valores entre 0 y 1 (que son justamente los valores entre los que se mueve la probabilidad).

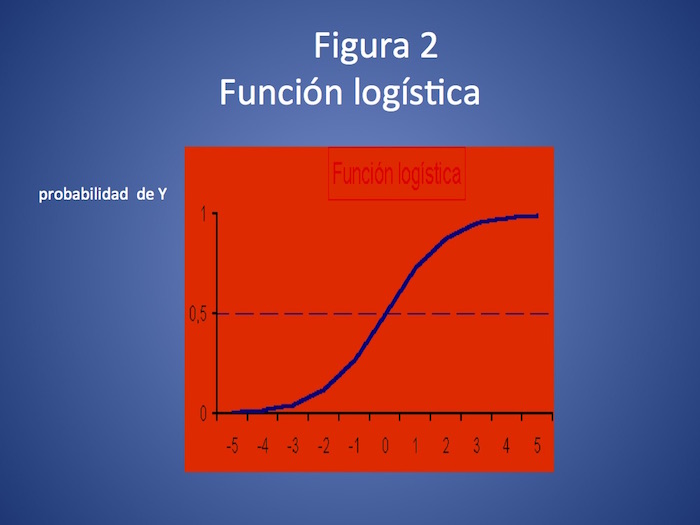
Para poder calcular la probabilidad de ocurrencia de una variable dicotómica tendremos que pasar por un estadio previo, el de considerar el concepto de odds y odds ratio (OR).

Debemos recordar que el concepto de odds y el de probabilidad están relacionados:

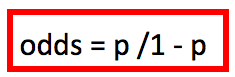
Y por lo tanto,

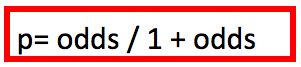
Por ejemplo, el odds de tener HTA, si la p de HTA es 0.33 es 0.333/0.666= 0.5

Y la probabilidad de tener HTA si el odds es 0, 5 es 0.5/ 1 + 0.5= 0.5/1.5 = 0.33

En lugar de recurrir a la regresión lineal, deberemos en este caso recurrir a la regresión logística.

Para entender bien de qué se trata deberemos refrescar primero el concepto de logaritmo. Tomemos como ejemplo los logaritmos decimales. En dicho sistema el número 10 es la base. Y el logaritmo es el número al que debemos elevar la base 10 para obtener un resultado determinado. Es decir que el logaritmo es la potencia de 10 que nos entrega un resultado. Por ejemplo, en el sistema de logaritmos decimales,

El logaritmo de 1 es 0, porque 10 elevado a la potencia 0 es 1.
El logaritmo de 10 es 1, porque 10 elevado a la potencia 1 es 10.
El logaritmo de 100 es 2, porque 10 elevado a la potencia 2 es 100.
El logaritmo de 2 es 0,30103, porque 10 elevado a la potencia 0,30103 es 2.

La regresión logística no trabaja con logaritmos decimales, lo hace con logaritmos naturales. En dicho sistema el número base se llama e, un número irracional cuyo valor aproximado es 2,7182818284… y sigue y sigue. El concepto de cualquier manera es el mismo que el de los logaritmos decimales. El logaritmo natural de un número es aquella potencia a la que hay que elevar e para lograr dicho resultado. Por ejemplo, en el sistema de logaritmos naturales

El logaritmo de 1 es 0, porque e elevado a la potencia 0 es 1
El logaritmo de 10 es 2,30…, porque e elevado a la potencia 2,30… es 10.
El logaritmo de 100 es 4,60…, porque e elevado a la potencia 4,60… es 100.

En la regresión logística, dada entonces una variable respuesta Y y una variable predictora X (y recordando que α es el valor de Y cuando X vale 0, y que β es cuánto cambia Y cuando X varía en una unidad) resulta (tras una serie de operaciones algebraicas) que el odds de Y está vinculado con la variable X por la expresión:

Si esto es así, entendemos que el logaritmo natural del odds es:

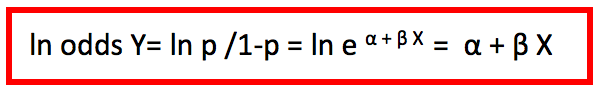
Repetimos: dadas las variables X e Y, si elevamos e a α +β X obtenemos el odds de Y. Por lo tanto, en el sistema de logaritmos naturales α +β X es el logaritmo natural del odds de Y.

A la expresión ln odds Y= ln p/1-p se la denomina logit p.

En la regresión lineal Y= α +β X. Esto implica que Y varía en forma lineal con X.

En la regresión logística ln odds de Y= logit p = α +β X. Esto implica que el ln odds de Y= logit de p varía en forma lineal con X.

En forma análoga a lo que habíamos visto en la regresión lineal:

α es el valor del ln odds Y cuando X vale 0

β es cuánto cambia el ln odds Y cuando X varía en una unidad.

Para entender entonces el sentido de lo que presentamos: la regresión lineal no permite definir probabilidad de una variable dicotómica. La regresión logística sí, pero para hacerlo necesita recurrir al odds. Al conocer el valor de X, α y β permite obtener el valor del ln odds, y por lo tanto, elevando e a dicho valor obtenemos el valor del odds.

Y como dijimos que

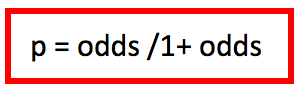
resulta claro que al conocer el odds podemos conocer el valor de la probabilidad. Como dividimos el valor del odds por dicho valor + 1, es claro que el resultado será siempre mayor que 0, y menor que 1, que es lo que buscábamos. En la próxima entrega completaremos los conceptos sobre regresión logística y veremos un ejemplo.

Dr. Jorge Thierer