¿Qué es la regresión logística? Parte 3

Antes de iniciar esta entrega, parece fundamental volver a leer las dos anteriores sobre el tema de regresión logística (Parte 1, y Parte 2). Repasemos algunos conceptos:

Cuando lo que buscamos es predecir la probabilidad de ocurrencia de una variable dicotómica recurrimos a la regresión logística.

La regresión logística trabaja con logaritmos naturales. En dicho sistema el número base se llama e, un número irracional cuyo valor aproximado es 2,7182818284….

En la regresión logística, dada entonces una variable respuesta Y y una variable predictora X (y recordando que en la regresión lineal α es el valor de Y cuando X vale 0, y que β es cuánto cambia Y cuando X varía en una unidad), el odds de Y está vinculado con la variable X por la expresión:

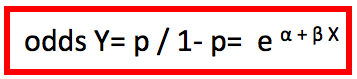
Entonces, el logaritmo natural del odds es

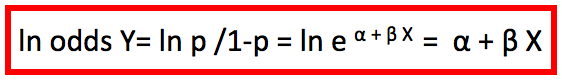
A la expresión ln odds Y= ln p/1-p se la denomina logit p.

Por lo tanto:

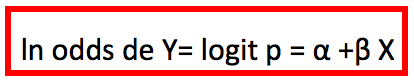
Y este es el secreto de la regresión logística:

α es el valor del ln odds Y cuando X vale 0

β es cuánto cambia el ln odds Y cuando X varía en una unidad.

Veamos un ejemplo.

Disponemos de una muestra de 150 pacientes, y de todos ellos tenemos el dato de la creatinina basa (en mg/dl), y del punto final internación por causa cardiovascular al año. Creatinina basal será nuestra variable predictora (X) e internación al año nuestra variable respuesta (Y). Internación al año es una variable dicotómica, por lo que para predecir probabilidad de internación al año conociendo la creatinina y la relación de riesgo (OR) a medida que la misma aumenta recurriremos a la regresión logística.

El programa de estadística, al vincular creatinina basal con internación el año nos dice que en este caso

α (lo que vale el ln del odds de Y cuando X vale 0) = – 1,78

β (cambio en el valor del ln odds Y por cada cambio de una unidad en X)= 1,47.

Si recordamos que ln odds de Y= logit p = α +β X (ver arriba), entonces

ln odds Y= logit p de internación si la creatinina es 1 mg/dl= -1,78 + (1,47 x 1) = – 0,31.

Y si elevamos el número e al ln que obtuvimos: e -0,31= 0,73.

Esto significa que el odds de internación cuando la creatinina es 1 mg/dl vale 0,73.

Y como p = odds / odds +1, resulta que

p de internación cuando creatinina vale 1 es 0,73 / 1,73= 0,42, o 42%.

¿Qué sucede si el valor de creatinina aumenta una unidad, esto es si es 2 mg/dl?

En este caso

ln odds Y= logit p de internación si la creatinina es 2 mg/dl= -1,78 + (1,47 x 2) = 1,16

Y si elevamos el número e al ln que obtuvimos: e -1,16= 3,19

Esto significa que el odds de internación cuando la creatinina es 2mg/dl vale 3,19.

Y como p = odds / odds +1, resulta que

p de internación cuando creatinina vale 2 es 3,19 / 4,19= 0,76, o 76%.

En resumen: si la creatinina vale 2 mg/dl, el odds de internación es 3,19, y si vale 1 mg/dl es 0,73.

La relación de riesgo de internación entre un valor de creatinina de 2 mg/dl y un valor de 1 mg/dl se expresa con el OR, o cociente de odds

OR = 3,19 / 0,73= 4,37.

¡Último esfuerzo!

Si averiguamos cuál es el ln de 4,37, veremos que es 1,47, nuestro coeficiente β!
O sea que e 1,47= 4,37

Es decir que finalmente

Si la variable X es continua, β es el cambio de ln OR al aumentar X en una unidad. Por ejemplo, lo que vimos: cuánto cambia el ln del OR al variar la creatinina en 1 mg/dl, o la glucemia en 1 mg/dl, o el sodio en 1 meq/l, etc.

Si la variable X es dicotómica (por ejemplo sexo masculino sí/no, diabetes sí/no), β es el cambio de ln OR con X presente (X=1) vs ausente (X=0).

En conclusión: la regresión logística permite, dada una variable predictora continua o dicotómica y una respuesta que siempre es dicotómica, averiguar el coeficiente β, y por lo tanto el OR vinculado con dicha variable predictora.

La regresión logística que establece el valor de β para cada predictor en forma aislada se llama regresión logística simple. Veremos más adelante el concepto de multivariabilidad y el rol que cabe a la regresión logística múltiple.

Dr. Jorge Thierer