¿Qué significa correlación?

Supongamos un estudio en que se investiga en un grupo de pacientes la asociación entre la función renal expresada en mg/dl de creatinina y la tensión arterial sistólica expresada en mm Hg. Ambas son variables continuas. Se puede generar entonces un gráfico donde en el eje de las abscisas se representan los valores de tensión arterial y en el de las ordenadas los de creatinina. A cada unidad de observación, cada paciente, corresponde un valor de creatinina y uno de tensión arterial.

Cada paciente, entonces, queda representado por un punto que señala la intersección entre ambos valores. De la representación de todos los pacientes surge una nube de puntos. Lo que se busca determinar es el grado de asociación lineal entre ambas variables. Es decir, si al aumentar los valores de una de ellas hay un aumento o decremento proporcional de la otra. Es fácil inferir que de existir una relación lineal se podrá predecir aproximadamente el valor de una de las variables ante una variación de la otra.

El estadístico que mide ese grado de asociación lineal es el coeficiente r. El coeficiente r no tiene unidades. Su valor oscila entre +1 y -1. Un valor de +1 implica una relación lineal ascendente perfecta: a cada magnitud de aumento de una de las variables corresponde la misma magnitud de aumento en la otra. Un valor de -1 implica una relación lineal descendente perfecta: a cada magnitud de aumento de una de las variables corresponde la misma magnitud de descenso en la otra.

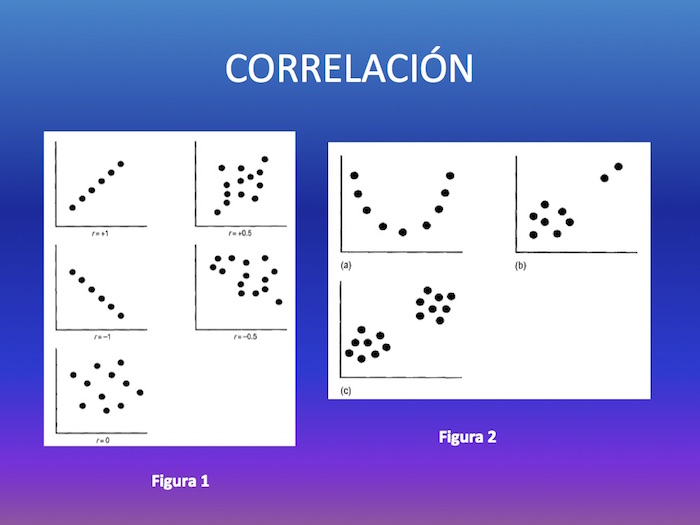
Valores de +1 ó -1 son lógicamente inhallables. Valores cercanos a estos extremos implican alto grado de asociación lineal. A medida que los valores de r se acercan a 0, el grado de asociación lineal entre las variables estudiadas es menor. Un coeficiente r de 0 implica ausencia absoluta de asociación lineal. Ejemplos de todas las situaciones descriptas se ven en la figura 1.

Como toda determinación estadística, a cada valor de r en cada situación corresponde un valor de p, que expresa la probabilidad de que el valor de r sea debido al azar. Es decir que no solo importa el valor de r, sino también el valor de p. Solo se acepta un valor de r como verdadero si su valor de p es < 0.05. Como con todo lo visto hasta aquí, el valor de p está influido por el tamaño de la muestra. Muestras pequeñas pueden presentar valores de r elevados (cercanos a +1 ó -1) pero con valor de p no significativo. De igual modo, valores de r de poca relevancia clínica pueden tener significación estadística si la muestra es numerosa.

Más allá de esta aclaración, los valores de r dan solo una valoración de si existe una asociación lineal, pero no una idea acabada de cuánto influye la variación en los valores de una de las variables en los valores de la otra. Para ello es necesario recurrir a R², que surge justamente de elevar al cuadrado el valor de r. R² es sí expresión del cambio que la variación de una variable importa en la otra. Por ejemplo, un valor de r de 0.5 implica un R² de 0.25. Esto significa que solo el 25% de la variación de los valores de una variable se debe a la variación de la otra.

De allí que solo un valor de r de 1, por lo tanto con un R² de 1, implica que toda la variación en una de las variables se explica por los cambios en la otra. Considerar R² más que r ayuda a poner las cosas en perspectiva. Muestras grandes pueden arrojar significación estadística para valores de r de escasa o nula relevancia clínica. En estos casos, sin embargo, el hallazgo de un valor de r significativo puede servir para encontrar una relación que tenga sentido fisiopatológico, o que contribuya a demostrar algún grado de asociación que justifique nueva investigación.

Es imprescindible mirar los gráficos de correlación y no quedarnos solamente con leer el valor de r. Que r no sea significativo no implica que no haya asociación entre las variables estudiadas. Implica que no hay asociación lineal. Una asociación no lineal (curva en J o en U) puede estar presente, con un gráfico que la demuestre y un valor de r sin significación estadística (figura 2, gráfico a).

En determinadas situaciones el valor de r puede ser significativo, pero en realidad el gráfico nos demuestra que las bases del hallazgo no son correctas. Se puede obtener un valor de r significativo al colocar conjuntamente 2 subgrupos en cada uno de los cuales no hay asociación lineal, pero que puestos conjuntamente generan un r significativo; escasos valores fuera de rango pueden también traccionar de la línea de correlación y simular una relación lineal (figura 2, gráficos b y c).

Los hallazgos de un estudio de correlación se aplican solamente al rango de valores estudiados. No se pueden extrapolar las conclusiones a valores de las variables por fuera de ese rango. Una relación lineal en el rango estudiado puede no mantenerse por fuera del mismo.

En resumen, al estudiar correlación debemos tener en cuenta el valor de r, el correspondiente valor de p, considerar el valor de R² y estudiar cuidadosamente el gráfico de la relación.

La palabra correlación suele ser mal empleada. Muchas veces escuchamos o leemos que la presencia de diabetes se correlaciona con la incidencia de IAM, o que mayor edad se correlacionó con el sexo femenino. En casos en que ambas variables no son continuas el término correcto es asociación.

Dr. Jorge Thierer