¿Qué son la hipótesis nula e hipótesis alternativa?

Frente a cualquiera de los casos citados en la última entrega es posible formular la hipótesis de que no hay diferencia entre el valor hallado y el de referencia, entre el valor de la media o proporción de una muestra y el de la población; o entre el valor en un grupo y en otro con el que se compara. No porque numéricamente sean lo mismo 1.18mg% y 1.35 mg% en el caso de las creatininas, o 40% y 33% en el de las prevalencias de hipertensión, sino porque se entiende que en cada situación forman parte de la misma distribución de probabilidades, y que por lo tanto es el azar el responsable de que hayamos encontrado valores diferentes. Si el azar nos llevó al hallazgo de valores diferentes dentro de la misma distribución, podemos concluir que no hay diferencia significativa entre los mismos. Esta hipótesis es la llamada hipótesis nula (H0).

Frente a la misma se alza la hipótesis alternativa (HA), que afirma que sí hay diferencia entre el valor hallado y el de referencia, o entre el de uno y otro grupo. Para esta hipótesis, entonces, los valores de creatinina de los internados con IAM o insuficiencia cardíaca son diferentes, no forman parte de la misma distribución, no son valores esperables de un mismo grupo, sino que corresponden a poblaciones diferentes.

¿Cómo decidir cuál de las 2 hipótesis es la correcta? Todo gira en relación de la hipótesis nula, y de rechazarla o no rechazarla. Un test estadístico especial para cada caso (comparación de medias, o de medianas, o de proporciones, o de varianzas) nos permitirá establecer, en la distribución de probabilidades correspondiente a la variable que estamos estudiando, dónde se encuentra la determinación que nos importa respecto de aquella con la que la estamos comparando; y aclarará si existe o no una diferencia estadísticamente significativa entre ambas. Dicho test nos dirá si en la distribución de probabilidades, respecto del valor del comparador, el que nos interesa está en área de no rechazo o de rechazo de la hipótesis nula. (figura)

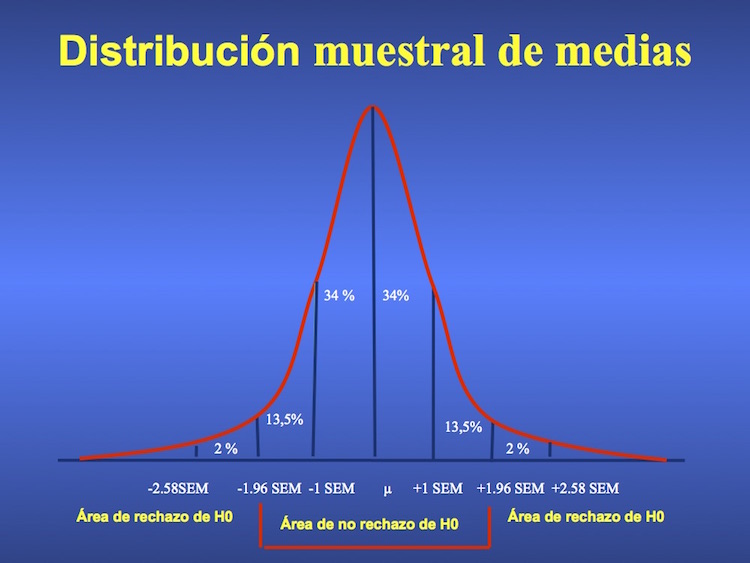
Por un criterio convencional se entiende que la hipótesis nula no se puede rechazar si la media o proporción hallada se encuentra dentro del 95% central de la distribución de probabilidades que tiene como media o proporción media a la poblacional, o a la del grupo comparador. Entendemos en este caso que la diferencia se debe al azar.

Si en cambio el valor encontrado se encuentra por fuera de ese 95%, si forma parte del 5% de valores extremos, está en la llamada área de rechazo, y la hipótesis nula es rechazada. Es como si una probabilidad menor del 5 % (p<0.05) de diferencia debida al azar fuera ya “demasiado poco” como para negar la diferencia. Por eso cuando en una comparación entre 2 valores el test informa que la probabilidad de que pertenezcan a la misma distribución es menor de 5%, decimos sí que la diferencia es estadísticamente significativa.

El valor de corte para rechazar la hipótesis nula (5 %, 1 en 20, p=0.05) es expresión de una convención. Con una probabilidad de 5.1% (p=0.051) de pertenecer a la misma distribución consideramos que la diferencia se debe al rol del azar, con una probabilidad de 4.9% (p= 0.049) lo rechazamos.

Otro hecho a tener en cuenta es que la hipótesis nula nunca se acepta; como vimos, se rechaza o no se rechaza. Ello tiene que ver con que aceptar la hipótesis nula significa afirmar definitivamente que no hay diferencia entre los valores comparados. Como veremos luego, puede ser que en realidad el número de observaciones no haya bastado para hacer notable una diferencia que existe; por eso es que sólo podemos limitarnos a no rechazar por el momento la hipótesis nula, pero no a aceptarla como verdad.

Dr. Jorge Thierer