¿Qué son y qué expresan el riesgo relativo y el odds ratio?

Como dijimos en la primera entrega de esta serie, en todo lo que leemos en investigación clínica existe una intención: demostrar que la existencia de una determinada condición (a la que llamaremos exposición) se traduce en la ocurrencia de una determinada evolución o evento. Tradicionalmente entendemos por exposición la presencia de una condición del entorno o de determinada patología (por ejemplo, contaminación ambiental con determinado compuesto, presencia de hipertensión arterial o cáncer de endometrio) y por evento un cuadro clínico preciso vinculado con la anterior (enfermedad pulmonar crónica, accidente cerebrovascular y muerte, respectivamente).

En cada uno de los casos presentados, el objeto inicial de investigación será determinar si la presencia de la exposición se asocia en forma estadísticamente significativa (y ello implica más allá del azar) con que ocurra el evento, con el resultado.

La variable que buscamos predecir en este tipo de estudio es dicotómica: algo sucede o no sucede. Querremos saber si hay variables basales cuya presencia o ausencia determina dicha ocurrencia.

Las medidas básicas de asociación de las variables predictoras con el resultado son el riesgo relativo y el odds ratio. Veamos un ejemplo.

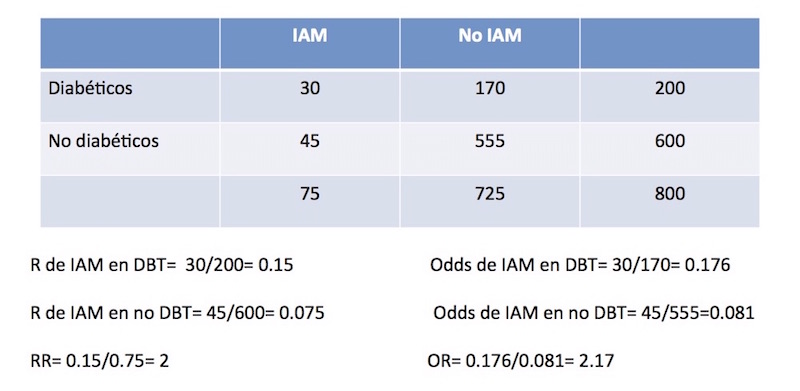
En una cohorte de 800 varones mayores de 45 años el 25% (n= 200) son diabéticos y el resto no lo es. En un seguimiento de 8 años presentan IAM 30 de los diabéticos y 45 de los no diabéticos. ¿Se asocia la diabetes a un riesgo mayor de presentar IAM que el hecho de no padecerla?

El riesgo de un diabético de presentar IAM en el seguimiento es igual a la proporción de diabéticos que presentan IAM sobre el total de los diabéticos: en este caso 30/200= 0.15. El riesgo de un no diabético de presentar IAM en el seguimiento es igual a la proporción de no diabéticos que presentan IAM sobre el total de los no diabéticos: en este caso 45/600= 0.075. El riesgo relativo (RR) de un diabético respecto de un no diabético de presentar IAM en el seguimiento es igual al cociente de los riesgos: 0.15/0.075= 2.

Quiere decir que en este estudio los diabéticos tienen el doble riesgo que los no diabéticos de infartarse.

Remarquemos 2 cosas:
a) El riesgo es una proporción: una parte sobre el total.
b) El RR es por lo tanto un cociente de proporciones. Señala cuánto más frecuentemente (si su valor es > 1) o menos frecuentemente (si su valor es <1) es posible esperar un resultado o evolución en un grupo respecto de otro.

El concepto de odds ratio es algo más difícil de aprehender, pero intentaremos que se entienda. La palabra odds se traduce en principio como posibilidad. El término odds se vincula también con ventaja, superioridad. ¿Cuál es la posibilidad de que algo suceda respecto de que no suceda?

Si volvemos a nuestra tabla, veremos que en los 200 diabéticos la chance de infartarse respecto de no infartarse es 30 /170: en 200 observaciones 30 posibilidades de infartarse frente a 170 de que ello no suceda. Este cociente, 30/ 170 es el odds de infartarse respecto de no hacerlo entre los diabéticos: su valor es entonces 0.176. Como vemos el odds es algo mayor que el riesgo, lo cual es lógico porque en el riesgo el denominador es el total de observaciones, y en el odds la cantidad de observaciones que no presentan el evento. Entre los 600 no diabéticos el odds para IAM será entonces 45/555=0.081. Y por lo tanto, el odds ratio (OR) de diabetes para IAM será el cociente de los odds: 0.176/ 0.081= 2.17.

Remarquemos que:

a) El odds es una razón (una parte respecto de la otra, no respecto del total).

b) El OR es por lo tanto un cociente de razones y no un cociente de proporciones, como el RR.

En la próxima entrega haremos consideraciones adicionales sobre RR y OR.

Dr. Jorge Thierer